华为上机题-3

发表于 | 阅读次数:

字符串处理

大数运算处理

1
2
3
4
5
6
7
8
题目描述
在计算机中，由于处理器位宽限制，只能处理有限精度的十进制整数加减法，比如在32位宽处理器计算机中，
参与运算的操作数和结果必须在-231~231-1之间。如果需要进行更大范围的十进制整数加法，需要使用特殊
的方式实现，比如使用字符串保存操作数和结果，采取逐位运算的方式。如下：
9876543210 + 1234567890 = ?
让字符串 num1="9876543210"，字符串 num2="1234567890"，结果保存在字符串 result = "11111111100"。
-9876543210 + (-1234567890) = ?
让字符串 num1="-9876543210"，字符串 num2="-1234567890"，结果保存在字符串 result = "-11111111100"。
1
2
3
4
5
输入描述:
输入两个字符串

输出描述:
输出给求和后的结果
1
2
3
4
5
6

输入
9876543210
1234567890
输出
11111111100

主要实现大数相加(进位)
大数相减(借位)
python解题代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
import sys
def BigNumAdd(Num1,Num2):
    A=map(int,list(Num1))
    B=map(int,list(Num2))
    L1=len(A)
    L2=len(B)
    A.reverse()
    B.reverse()
    if L1>L2:
        Max=A
        Min=B
    else:
        Max=B
        Min=A
    jinwei=0
    d=list()
    for i in range(len(Min)):
        jinwei=Min[i]+Max[i]+jinwei
        baoliu=jinwei%10
        jinwei=jinwei/10
        d.insert(0,str(baoliu))
        if i==len(Min)-1 and jinwei>0 and L1==L2:
            d.insert(0,str(jinwei))
    if L1!=L2:
        for i in range(len(Min),len(Max)):
            baoliu=jinwei+Max[i]
            jinwei=baoliu/10
            baoliu=baoliu%10
            d.insert(0,str(baoliu))
            if i==len(Max)-1 and jinwei>0:
                d.insert(0,str(jinwei))
    
    d=''.join(d)
    
    return d


def BigNumSub(Num1,Num2):
    Max=max(Num1,Num2)
    Min=min(Num1,Num2)
    if Max==Min:
        return '0'
    
    Max=map(int,list(Max))
    Min=map(int,list(Min))
    Max.reverse()
    Min.reverse()
    d=list()
    jiewei=0
    for i in range(len(Min)):
        baoliu=Max[i]-Min[i]-jiewei
        if baoliu<0:
            baoliu=baoliu+10
            jiewei=1
        else:
            jiewei=0
        d.insert(0,str(baoliu))
    d=''.join(d)
    return d

def func(Num1,Num2):
    if Num1[0]=='-' and Num2[0]=='-':
        a=Num1[1:]
        b=Num2[1:]
        r='-'+BigNumAdd(a,b)
    elif Num1[0]!='-' and Num2[0]!='-':
        r=BigNumAdd(Num1,Num2)
    else:
        M=max(Num1,Num2)
        T=min(Num1,Num2)
        flag=0
        if T[1:]>M:
            flag=1
        r=BigNumSub(T[1:],M)
        if flag==1:
            r='-'+r
    return  r
                
while True:
    try:
        num1=sys.stdin.readline().strip()
        num2=sys.stdin.readline().strip()
        r=func(num1,num2)
        print r
    except:
        break

进制转化

1
2
3
4
5
6
7
8
题目描述
写出一个程序，接受一个十六进制的数值字符串，输出该数值的十进制字符串。（多组同时输入 ）

输入描述:
输入一个十六进制的数值字符串。

输出描述:
输出该数值的十进制字符串。
1
2
3
4
5
示例1
输入
0xA
输出
10

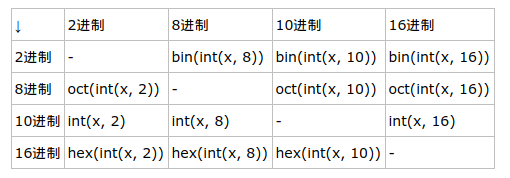
进制转化函数.png
需要注意的是输入的x必须是数字类型,不能是字符了;类型
bin()、oct()、hex()的返回值均为字符串，且分别带有0b、0o、0x前缀。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import sys

def  numChange(Num):
    T=list(Num[2:])
    T.reverse()
    sum=0;
    for i in range(len(T)):
        if T[i].isalpha():
            t=ord(T[i])-ord('A')+10
        else:
            t=int(T[i])
        sum+=t*(16**i)
    return sum
    



while True:
    try:
        st=raw_input()
        r=numChange(st)
        print r
    except:
         break

关于牛客网中的sys.stdin.readline().strip()和raw_input()输入函数,优先选择raw_input,会把换行符去掉,通过概率更高!!!!
用内置函数int

1
2
3
4
5
while True:
	try:
    	print int(raw_input(),16)
   	except:
    	break

字符串加密

1
2
3
4
5
6
7
8
9
10
题目描述
有一种技巧可以对数据进行加密，它使用一个单词作为它的密匙。下面是它的工作原理：首先，选择一个单词作为密匙，如TRAILBLAZERS。如果单词中包含有重复的字母，只保留第1个，其余几个丢弃。现在，修改过的那个单词属于字母表的下面，如下所示：

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

T R A I L B Z E S C D F G H J K M N O P Q U V W X Y

上面其他用字母表中剩余的字母填充完整。在对信息进行加密时，信息中的每个字母被固定于顶上那行，并用下面那行的对应字母一一取代原文的字母(字母字符的大小写状态应该保留)。因此，使用这个密匙，Attack AT DAWN(黎明时攻击)就会被加密为Tpptad TP ITVH。

请实现下述接口，通过指定的密匙和明文得到密文。
1
2
3
4
5
6
7
8
9
10
11
12
输入描述:
先输入key和要加密的字符串

输出描述:
返回加密后的字符串

示例1
输入
nihao
ni
输出
le

代码实现的时候需要注意字母大小写的统一化,统一成大写就方便了
自己的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import sys
def generateKey(S1):
    S=S1.upper()
    L=list()
    for i in S:
        if i in L:
            continue
        else:
            L.append(i)
    d={}
    index=0
    for i in L:
        t=chr(ord('A')+index)
        index+=1
        d[t]=i
    M=list()
    for i in range(26):
        t=chr(ord('A')+i)
        if t in L:
            continue
        else:
            M.append(t)
    for i in M:
        t=chr(ord('A')+index)
        index+=1
        d[t]=i
    return d

def encode(S1,d):
    S=S1.upper()
    r=list()
    for i in S:
        t=d[i]
        r.append(t.lower())
    r=''.join(r)
    return r
while True:
    try:
        k=raw_input()
        c=raw_input()
        d=generateKey(k)
        r=encode(c,d)
        print r
    except:
        break;

别人的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
while True:
    try:
        lineCode , line = raw_input() , raw_input()
        code = []
        res = ''
        for i in lineCode:
            if i not in code:
                code.append(i)
        for i in range(97,123):
            if chr(i) not in code:
                code.append(chr(i))
        for i in line:
            res += code[ord(i)-97]
        print res
    except:
        break

尼克切斯定理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
题目描述
验证尼科彻斯定理，即：任何一个整数m的立方都可以写成m个连续奇数之和。

例如：

1^3=1 

2^3=3+5 

3^3=7+9+11 

4^3=13+15+17+19 
------------------------------------------------
输入描述:
输入一个int整数

输出描述:
输出分解后的string

示例1
输入
6
输出
31+33+35+37+39+41

这道题的解法就是求出中位数,确定前后位置遍历一遍解就出来了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def Fenjie(N):
    t=int(N)
    T=t**3
    Ave=T/t
    d=list()
    if t%2==0:
        St=Ave-t+1
        Et=Ave+t-1
    else:
        St=Ave-t+1
        Et=Ave+t-1
    for i in range(St,Et+2)[::2]:
        d.append(str(i))
    
    r='+'.join(d)
    return r

while True:
    try:
        n=int(raw_input())
        r=Fenjie(n)
        print r
    except:
        break

火车进站问题

1
2
3
4
5
6
7
题目描述
给定一个正整数N代表火车数量，0<N<10，接下来输入火车入站的序列，一共N辆火车，每辆火车以数字1-9编号。要求以字典序排序输出火车出站的序列号。 
输入描述:
有多组测试用例，每一组第一行输入一个正整数N（0<N<10），第二行包括N个正整数，范围为1到9。

输出描述:
输出以字典序从小到大排序的火车出站序列号，每个编号以空格隔开，每个输出序列换行，具体见sample。
1
2
3
4
5
6
7
8
9
10
示例1
输入
3
1 2 3
输出
1 2 3
1 3 2
2 1 3
2 3 1
3 2 1
1
2
3
4
5
这道题问题的描述进一步解释是就是A[1..9]中转到C,C再转到B
产生的序列,其中只能从A-C,C-B,不存在类似序列
这个问题如果用python解的话很好解,A是压满的栈,从1到9栈顶到栈底,A只能pop
但是C能push,也能pop,B只能push,A pop的时候,C只能push,C pop的时候,B push
只有当A,C全部pop为空的时候,序列就产生了

python的解法相当清晰
A–>C
C–>B

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import copy

result=list()

def func(A,C,B):
    if len(A)==0 and len(C)==0:
        result.append(' '.join(B))
    else:
        if len(C)>0:
            temp_A=copy.deepcopy(A)
            temp_C=copy.deepcopy(C)
            temp_B=copy.deepcopy(B)
            temp_B.append(temp_C.pop())
            func(temp_A,temp_C,temp_B)
        if len(A)>0:
            temp_A=copy.deepcopy(A)
            temp_C=copy.deepcopy(C)
            temp_B=copy.deepcopy(B)
            temp_C.append(temp_A.pop(0))
            func(temp_A,temp_C,temp_B)

while True:
    try:
        n=int(raw_input())
        st=raw_input().split()
        pre=st
        In=[]
        After=[]
        func(pre,In,After)
        result.sort()
        for rs in result:
            print rs
    except:
        break

热评文章